递归算法及经典递归实现

发表于 | 分类于 | 热度:
字数统计: 3.6k 字 | 阅读时长 ≈ 14 分钟

# 递归

递归就是方法自己调用自己，每次调用时传入不同的变量，递归有助于编程者解决复杂的问题，同时可以让代码变得简洁。

递归： 在定义自身的同时又出现了对自身的调用
直接递归函数： 在定义函数体中直接调用自己
间接递归函数： 一个函数经过一系列中间调用语句，通过其他函数调用自己，如P调用Q，Q再调用P

使用 递归算法的 前提有两个：
（1） 原问题可以层层分解为类似的子问题，且子问题比原问题的规模更小。
（2）规模更小的子问题具有直接解

设计递归算法的原则是用自身的简单情况来定义自身设计递归算法的方法是：
（1）寻找分解方法，将原问题转化为子问题求解
（2）设计递归出口，也就是说根据最小的子问题，确定递归终止的条件。

递归过程的实现

递归的过程 ，递归进程和递归退层。
递归进程，也就是说递归的过程 i 到 i+1 层，系统需要做三件工作：
（1）保留本层参数与返回地址；
（2）给下层参数赋值
（3）将程序转移到被掉函数的入口

递归退层：也就是从i+1层到i层，系统也应该完成三件工作
（1）保留被调函数的计算结果
（2）恢复上层参数，也就是释放被调函数的数据区
（3）依照被调函数保存的返回地址，将控制转移回调用函数。、

递归函数的运行，以及递归中进层退层的实现，都需要递归机制的支持。

什么是递归机制？

递归机制支持？

系统设置一个递归工作栈作为递归函数运行使用的存储区，每次递归需要所需信息构成一个工作记录，包括实参，局部变量以及上一层的返回地址。每进入一层递归，就产生一个新的工作记录压入栈顶，每退出一层递归，就从栈顶弹出一个工作记录。

我们可以通过一个简单的阶乘例子来看一下递归调用机制的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
package com.recusion;

public class printDemo {

	public static void main(String[] args) {
		test(4);
	}
	
	public static void test(int n){
		if (n>2) {
			test(n-1);
		}
		System.out.println("n="+n);
	}
	
}

当我们的程序执行的时候，首先进入的是主方法。
具体过程我们可以通过虚拟机的调用顺序来看一下详细过程

Java虚拟机主要分成三个部分：
栈空间，堆空间，另外还有一个空间是代码区包括常量
在这里插入图片描述
我们的程序执行到主方法的时候，会首先在栈中开辟一个空间 ，这个空间我们可以叫做main[ 栈 ]，在这里面调用了 test(4),根据调用规则，会另外开辟新栈。n=4 ，会进行判断，n>2时，又执行test(3) ，当执行到这里的时候，下面的代码不会执行，仍然会开辟一个新的栈，继续进行判断，test（2），进行判断，然后继续开辟新的栈。继续判断，不符合之后会执行下面的指令。（会首先执行顶级的栈）所以首先会在控制台输出n=2，
执行完之后弹出，继续执行下面的栈。

执行过程：图解如下

在这里插入图片描述

递归调用规则：

  1. 当程序执行到一个方法时，就会开辟一个独立的空间(栈)
  2. 每个空间的数据（局部变量）是独立的，由上面的过程我们可以发现，在每一个栈中，我们都有一个局部变量n=4，n=3….这些局部变量之间是相互独立的。

下面我们来看一下，递归实现阶乘的例子：

1
2
3
4
5
6
7
8
//阶乘问题
public static int factorial(int n){
	if (n == 1) {
		return 1;
	}else {
		return factorial(n-1)*n;
	}
}

递归能解决的问题？

  1. 各种数学问题，如8皇后，汉诺塔，阶乘问题，迷宫问题，球和篮子的问题（Google编程大赛）
  2. 各种各种算法也会用到递归，比如归并排序，二分查找，分治算法等
  3. 将用栈解决的问题，使用递归解决比较简单

递归使用时需要遵守的重要规则

递归需要在遵守的重要规则：

  1. 执行一个方法时，就是创建一个新的受保护的独立空间（栈空间）
  2. 方法的局部变量是独立的，不会相互影响，比如上面例子中的n变量，在每一个栈空间中是独立的。
  3. 如果方法中使用的是引用类型变量，比如说是数组，就会共享该引用类型的数据
  4. 递归必须向退出递归的条件逼近，否则就是无限递归，进入死循环。
  5. 当一个方法执行完毕，或者是遇到return。就会返回，遵守谁调用，就将结果返回给谁，同时当方法执行完毕或者返回时，该方法也就执行完毕。

递归经典算法

迷宫问题

迷宫问题说明：
1）小球得到的路径，和程序员设置的找路策略有关，即找路的上下左右的顺序相关
2）再提到小球路径时，可以先使用（下右上左），再改成（上右下左），看看路径是不是有变
3）测试回溯现象

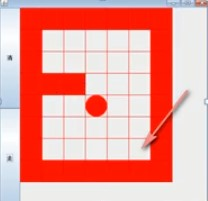
在这里插入图片描述
小球得到的路径，和程序设置的找路径策略有关：即找路的上下左右的顺序有关，在得到小球的路径时，可以先使用 下-右—上–左 ，如果不行再改用 上–右–下–左 ， 看看路径是不是有变化，测试回溯现象（我们可以多增加几个墙，这样可以测试回溯现象）。

Q：如何求出最短的路径？

我们可以使用递归进行实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
package com.recusion;

public class MiGong {

	public static void main(String[] args) {
		//先创建一个二维数组，模拟迷宫
		//写一个地图，用二维数组表示地图8行7列的二维数组
		int[][] map = new int[8][7];
		//在地图中我们使用1表示墙
		//上下全部置为1
		for (int i = 0; i < 7; i++) {
			map[0][i] =1;
			map[7][i] =1;
		}
		
		//左右全部置为1
		for(int i = 0; i < 8;i++){
			map[i][0] = 1;
			map[i][6] = 1;
		}
		map[3][1]=1;
		map[3][2]=1;
		
		//输出地图
		for(int i = 0;i<8;i++){
			for(int j=0;j<7;j++){
				System.out.print(map[i][j]+" ");
			}
			System.out.println();
		}
		
		//使用递归回溯给小球找路
		setWay(map, 1, 1);
		
		//输出地图，小球走过，并标识过的地图
		System.out.println("地图的情况，走过标记过的地图");
		for(int i = 0;i<8;i++){
			for(int j=0;j<7;j++){
				System.out.print(map[i][j]+" ");
			}
			System.out.println();
		}
		
		
	}
	
	
	//使用递归回溯来给小球找路
	//说明
	//1. map 表示地图
	//2. i,j 表示从地图的哪个地方开始出发（1,1）
	//3. 如果小球能到 map[6][5] 位置，则说明通路找到
	//4. 约定：当map[i][j] 为0表示该点没有走过，当为1表示墙,当为2时是通路可以走的，为3表示该位置已经走过但是走不通
	//5. 在走迷宫时需要确定一个策略，也就是一个规则，先走下面，下面不同，再走右面，右面不同在走上面，上面不通，再走左面。如果该点走不通，再回溯
	/**
	 * 	1 1 1 1 1 1 1 
		1 0 0 0 0 0 1 
		1 0 0 0 0 0 1 
		1 1 1 0 0 0 1 
		1 0 0 0 0 0 1 
		1 0 0 0 0 0 1 
		1 0 0 0 0 0 1 
		1 1 1 1 1 1 1 
	 */
	/**
	 * map表示地图
	 * i，j表示从 哪个位置开始找
	 * 如果找到通路返回true，如果找不到返回false
	 * @return
	 */

	public static boolean setWay(int[][] map,int i,int j){
		
		if(map[6][5] ==2 ){
			return true;
		}else {
			if (map[i][j] == 0) {//如果当前点还没有走过
				//按照策略走
				map[i][j] = 2;//假定该点可以走通
				if (setWay(map, i+1, j)) {//先向下走
					return true;
				}else if (setWay(map, i, j+1)) {//向右走
					return true;
				}else if(setWay(map, i-1, j)){//向上走 
					return true;
				}else if(setWay(map, i, j-1)){//向左走
					return true;
				}else {
					//下右上左都走不通，说明这个点是不同的，
					map[i][j]=3; //标记为此路不同别走
					return  false;
				}
				
			}else{//如果该点不等于0，map可能是1,2,3  1表示墙，2 走过了  3 是死路
				return false;
				
			}
		}
		
	}	
	
}
递归经典算法八皇后问题：回溯算法

八皇后问题介绍;
八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。在8*8格的国家象棋上摆放八个皇后，使其不能互相攻击，即：任意两个皇后都不能处于同一行，同一列，或者是同一斜线上，问有多少中摆法？
解法：我们可以使用回溯法进行解决。

八皇后问题算法思路分析：
（1） 第一个皇后先放第一行第一列
（2） 第二个皇后放在第二行的第二列，然后判断是否OK，即是判断是否冲突，如果不OK，继续放在第二列，第三列，依次把所有的列都放完，找到一个合适的。
（3） 继续第三个皇后，还是第一列，第二列…..直到第8个皇后也能放在一个不冲突的位置，算是找到了一个正确解。
（4）当得到一个正确解时，在栈回退到上一个栈时，就会开始回溯，即将第一个皇后，放到第一列的所有正确解全部得到。
（5）然后回头继续将第一个皇后放到第二列，后面继续循环执行1,2,3的步骤

需要说明的是，理论上需要创建一个二维数组表示棋盘，但是实际上可以通过算法，用一个一维数组即可解决问题。
（也就是经过分析，我们先找出一个可能的解，在每一行中填上数组的下标，当前位置表示已经放上皇后， {0,4,7,5,2,6,1,3} 表示提前在此位置上放上八个皇后）
arr[8] = {0,4,7,5,2,6,1,3} 对应的数组下标表示的是第几行，即第几个皇后，arr[i] = val ， val表示第i+1个皇后，放在第i+1行的第val+1列。

编程思路：

  1. 定义一个数组，用于保存皇后放置位置的结果，比如 arr = {0， 4 ，7，5，2，6，1，3}

  2. 编写一个方法，放置第n个皇后check()，

  3. 查看当我们放置第n个皇后，就去检测该皇后和前面已经摆放好的皇后冲突

【说明】
【n 表示第n个皇后，n从0开始，arr[i] = val val的值表示第几个皇后，例如 {0,4,7,5,2,6,1,3} 中，4表示第2个皇后在第四列。（通过在这里我们可以发现，arr数组中里面存放的是列数，然后arr[n] 代表的是这个皇后在的列数 ）
我们需要进行位置 判断，首先判断两个元素是否是在同一行，然后进行是否在同一行进行判断，但是我们提前定义数组的时候，使用的是一维数组表示位置，按照这种方法定义，我们就可以使用array[i] == array[n] 进行是否值在同一行进行判断。然后还需要判断是否是在同一列进行判断，使用两个位置连线的斜率绝对值等于1进行判断 】

写一个方法，可以将皇后摆放的位置输出
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

package com.recusion;

public class Queen8 {
	
	//首先定义表示共有多少个皇后
	int  max =8;
	static int count=0;//用于统计总方案数
	//定义数组array，保存皇后放置位置的结果，比如 arr = {0,4,7,5,2,6,1,3}
	int[] array = new int[8];
	
	public static void main(String[] args) {
		Queen8 queen8 = new Queen8();
		queen8.check(0);
		System.out.println("一共有解法"+count);
		
	}
	
	
	// 放置皇后，编写一个方法，放置第n个皇后
	//特别注意，check是每一次递归时，进入到check中都有一套for循环for (int i = 0; i < max; i++) 因此会有回溯
	
	private void check(int n){
		if (n==max) { //n=8表示放置到第九个皇后，8个皇后已经放好
			print();
			return;
		}
		
		//依次放入皇后，并判断是否是冲突的
		for (int i = 0; i < max; i++) {
			array[n]=i;
			//判断当放置第n个皇后到i列时，判断是否是冲突的
			if (judge(n)) {
				//接着放n+1个皇后，即开始递归
				check(n+1); //如果有8个皇后，每一层都会遍历8个列，会产生回溯现象的
			}
			//如果冲突，就继续执行array[n] =i ;即将第n个皇后，放置在本行的后移一个位置
		}
		
	}
	
	
	
	//检测位置  编写方法，当我们放置第n个皇后时，就去检测该皇后是否和前面已经摆放好的皇后位置是否冲突
	/**
	 * n 表示第几个皇后
	 * @param n
	 * @return
	 */
	private boolean judge(int n){
		for(int i=0;i<n;i++){
			
			/**
			 * 说明
			 * 1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
			 * 2. Math.abs(n-i)== Math.abs(array[n]-array[i]) 表示判断第n个皇后是否和第i个皇后在同一斜线上
			 * n = 1 放置第二列为1， n=1时，array[1]=1
			 * Math.abs(1-0) ==1 Math.abs(array[n]-array[i]) = Math.abs(1-0) =1
			 * 3. 判断是否在同一行，这一个不用判断，因为for循环中直接限制过了，没有必要进行判断了
			 */
			
			if (array[i]==array[n] || Math.abs(n-i)== Math.abs(array[n]-array[i])) {
				return false;
			}	
		}
		return true;
	}
	
	//写一个打印数据，也就是皇后放置位置的方法
	private void print(){
		count++;
		for (int i = 0; i < array.length; i++) {
			System.out.print(array[i]+" ");
		}
		System.out.println();
	}
	
}

本文标题:递归算法及经典递归实现

文章作者:雷凯博

发布时间:2019年08月10日 - 10:08

最后更新:2021年05月16日 - 19:05

原始链接:http://yoursite.com/2019/08/10/%E9%80%92%E5%BD%92%E7%AE%97%E6%B3%95%E5%8F%8A%E7%BB%8F%E5%85%B8%E9%80%92%E5%BD%92%E5%AE%9E%E7%8E%B0/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

坚持原创技术分享，您的支持将鼓励我继续创作！
-------------本文结束感谢您的阅读-------------
0%