SVM与KNN分类算法（wine数据集）

本片文章是使用分类算法KNN,和SVM支持向量机分类算法，对Wine数据集进行分类的实现。

1.1 wine数据集

Wine葡萄酒数据集是来自UCI上面的公开数据集，这些数据是对意大利同一地区种植的葡萄酒进行化学分析的结果，这些葡萄酒来自三个不同的品种。该分析确定了三种葡萄酒中每种葡萄酒中含有的13种成分的数量。从UCI数据库中得到的这个wine数据记录的是在意大利某一地区同一区域上三种不同品种的葡萄酒的化学成分分析。数据里含有178个样本分别属于三个类别，这些类别已经给出。每个样本含有13个特征分量(化学成分)，分析确定了13种成分的数量，然后对其余葡萄酒进行分析发现该葡萄酒的分类。

数据集中包含两个数据文件
Wine.data 包含所有数据的数据文件
Wine.names 数据集描述文件
我对这些数据集的处理，以及数据集分析和分类实现使用的环境是MATLAB R2017a。

1.2 wine数据集属性描述

在wine数据集中，这些数据包括了三种酒中13种不同成分的数量。文件中，每行代表一种酒的样本，共有178个样本；一共有14列，其中，第一个属性是类标识符，分别是1/2/3来表示，代表葡萄酒的三个分类。后面的13列为每个样本的对应属性的样本值。剩余的13个属性是，酒精、苹果酸、灰、灰分的碱度、镁、总酚、黄酮类化合物、非黄烷类酚类、原花色素、颜色强度、色调、稀释葡萄酒的OD280/OD315、脯氨酸。其中第1类有59个样本，第2类有71个样本，第3类有48个样本。
具体属性描述如下表：

1.3 原始数据集展示

原始数据文件是wine.data形式的文件，这些data文件的内容是以纯文本和逗号分隔格式编码的数据。该类型文件为使用者提供了很好的分析功能，有助于实时数据研究，存储，管理和分析。
这里只展示原始数据文件中前20条数据。

1.4数据处理

由于我们下载的源数据中可能存在各种各样的数据，因此不经任何处理就进入处理数据很可能违背数据质量三要素的要求。用这样的数据在进行后续的数据挖掘，其可靠性可能会有很大的偏差。我们首先需要做的就是处理数据中的缺失数据或异常值。我们需要提高数据质量，对下载的原始数据进行数据清理过程。
首先进行的数据清洗的步骤相对较为简单与清晰，第一步需要进行偏差检测，即检查导致偏差的因素，并识别离散值与噪声值。然后进行数据清洗，即处理缺失值与噪声。在本数据集中由于数据都是连续的，而且通过对数据集的分析可以发现，数据集中一共有178个样本，由于数据源文件中的每个样本的数据都是完整的，没有空缺值等，所以我没有对该数据源文件进行数据的清理工作。
原始数据集中是178个样本值，14列属性值，但是第一列是类别标识号，所以我们需要把这一列数据拿出单独作为对比列，作为一个1781的矩阵。然后把剩余的属性作为一个待处理17813的矩阵。类别标识符为3，属性列为字符串我们也需要单独拿出作为一个13*1的属性矩阵。

Matlab数据分列处理

load wine.data
wine=wine(:,[2:14]);
wine_labels=wine(:,1);
save  wine wine_labels

处理后的数据集形式为下图所示，篇幅限制，只展示部分数据集。

1.5 KNN分类算法实现

1.5.1 KNN算法描述

k-近邻（kNN，k-NearestNeighbor）算法是一种基本分类与回归方法，KNN算法的指导思想是“近朱者赤，近墨者黑”，由你的邻居来推断出你的类别。先计算待分类样本与已知类别的训练样本之间的距离，找到距离与待分类样本数据最近的k个邻居；再根据这些邻居所属的类别来判断待分类样本数据的类别。K-近邻算法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。k-邻算法假设给定一个训练数据集，其中的实例类别已定。分类时，对新的实例，根据其k个最近邻的训练实例的类别，通过多数表决等方式进行预测。因此，k近邻算法不具有显式的学习过程即属于有监督学习范畴。k近邻算法实际上利用训练数据集对特征向量空间进行划分，并作为其分类的“模型”。k值的选择、距离度量以及分类决策规则是k近邻算法的三个基本要素。
KNN算法流程如下：
就是在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，在KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离。
其算法的描述为：

• 1）计算测试数据与各个训练数据之间的距离；
• 2）按照距离的递增关系进行排序；
• 3）选取距离最小的K个点
• 4）确定前K个点所在类别的出现频率；
• 5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

1.5.2 实验设计

（1）训练集和测试集的划分
为了提高分类的准确率，以及实验的正常验证，需要对训练集和测试集进行划分。将第一类的1-30，第二类的60-95，第三类的131-153做为训练集，相应的训练集的标签也要分离出来，将第一类的31-59，第二类的96-130，第三类的154-178做为测试集，相应的测试集的标签也要分离出来。具体代码如下所示。

% 将第一类的1-30，第二类的60-95,第三类的131-153做为训练集
train_data = [wine(1:30,:);wine(60:95,:);wine(131:153,:)];
train_label = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)];
% 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集
test_data = [wine(31:59,:);wine(96:130,:);wine(154:178,:)];
test_label = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)];

数据归一化
归一化的目的就是使得预处理的数据被限定在一定的范围内比如[0,1]或者[-1,1]，从而消除奇异样本数据导致的不良影响。如果不进行归一化，那么由于特征向量中不同特征的取值相差较大，会导致目标函数变“扁”。这样在进行梯度下降的时候，梯度的方向就会偏离最小值的方向，走很多弯路，即训练时间过长。在本实验中使用的数据归一化的方法是mapminmax方法，这是MATLAB自带的归一化函数。在这里使用，用作本数据集中数据的归一化，数据预处理,将训练集和测试集归一化到[0,1]区间。

数据归一化方法如下：

[mtrain,ntrain] = size(train_data);
[mtest,ntest] = size(test_data);
dataset = [train_data;test_data];
[dataset_scale,ps] = mapminmax(dataset',0,1);
dataset_scale = dataset_scale';
train_data = dataset_scale(1:mtrain,:);
test_data = dataset_scale( (mtrain+1):(mtrain+mtest),: );

归一化之后的数据形式如下：
归一化后训练集：

归一化后测试集：

归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为纯量。归一化为了加快训练网络的收敛性，以上是对数据归一化之后的展示。

（2）KNN过程

核心代码，
% 选定训练集和测试集
% 将第一类的1-30,第二类的60-95,第三类的131-153做为训练集
train_data = [wine(1:30,:);wine(60:95,:);wine(131:153,:)];
train_label = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)];
% 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集
test_data = [wine(31:59,:);wine(96:130,:);wine(154:178,:)];
test_label = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)];
 
mdl = ClassificationKNN.fit(train_data,train_label,'NumNeighbors',1);
predict_label   =   predict(mdl, test_data);
accuracy    =  length(find(predict_label == test_label))/length(test_label)*100

程序运行之后，生成的预测标签如下，左侧为预测分类标签，右侧为实际测试分类标签。

)
1）未进行数据归一化
我使用Matlab中的KNN算法进行数据集的分析与实验。首先是未进行数据归一化的数据结果。

分类准确率为70.7865%。

2）数据归一化
通过上述分类结果我们发现，正确率只有百分之70左右，分类结果正确率比较低。然后，我使用mapminmax方法对数据进行归一化，归一化之后的数据结果如下所示。

1.5.3 实验结果与分析

为了更加直观的看到数据效果，对分类结果使用饼状图，以及曲面图进行展示，提供数据的可视化效果。这里展示的是数据归一化之后的分类结果。

分类结果在曲面图上展示如下：

1.6 SVM算法分类实现

1.6.1 SVM算法描述

SVM（support Vector Mac）又称为支持向量机，是一种二分类的模型。支持向量机可以分为线性核非线性两大类。支持向量机的主要思想是建立一个最优决策超平面，使得该平面两侧距离该平面最近的两类样本之间的距离最大化，从而对分类问题提供良好的泛化能力。对于一个多维的样本集，系统随机产生一个超平面并不断移动，对样本进行分类，直到训练样本中属于不同类别的样本点正好位于该超平面的两侧，满足该条件的超平面可能有很多个，SVM正式在保证分类精度的同时，寻找到这样一个超平面，使得超平面两侧的空白区域最大化，从而实现对线性可分样本的最优分类。
SVM的核心思想可以概括为两点：
（1）它是针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分，从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。
（2）它基于结构风险最小化理论之上再特征空间中构建最优超平面，使得学习器得到全局最优化，并且在整个样本空间的期望以某个概率满足一定上界。

1.6.2 SVM实验设计

（1）数据集的划分
在本实验中，数据集测试集和预测集的划分依旧使用的是上一节中的划分方法。将第一类的1-30,第二类的60-95,第三类的131-153做为训练集，相应的训练集的标签也分离出来，将第一类的31-59,第二类的96-130,第三类的154-178做为测试集，相应的测试集的标签也要分离出来。
（2）数据可视化
为了更加直观的看数据集中数据的分布情况，首先画出测试数据的分维可视化图进行数据情况展示。

从上面三个图中，我们可以看到数据集中数据的分布情况，各个属性范围的取值情况，但是我们并不能直观的得出分类结果，所以我们需要对数据进行更进一步的分析。

（3）数据归一化

归一化代码：
% 数据预处理,将训练集和测试集归一化到[0,1]区间
[mtrain,ntrain] = size(train_wine);
[mtest,ntest] = size(test_wine);
dataset = [train_wine;test_wine];
[dataset_scale,ps] = mapminmax(dataset',0,1);
dataset_scale = dataset_scale';
train_wine = dataset_scale(1:mtrain,:);
test_wine = dataset_scale( (mtrain+1):(mtrain+mtest),: );

%% SVM网络训练
%% SVM网络训练
model = libsvmtrain(train_wine_labels, train_wine, '-c 2 -g 1');
%% SVM网络预测
[predict_label, accuracy, libsvm_options] = libsvmpredict(test_wine_labels, test_wine, model);
%% 结果分析
 
% 测试集的实际分类和预测分类图
figure;
hold on;
plot(test_wine_labels,'X');
plot(predict_label,'r*');
xlabel('测试集样本','FontSize',12);
ylabel('类别标签','FontSize',12);
legend('实际测试集分类','预测测试集分类');
title('测试集的实际分类和预测分类图','FontSize',12);
grid on;

1.6.3 结果分析与展示

运行结果：
运行以上程序，我们可以发现如果不使用数据归一化对数据进行处理分类正确率只有39%。

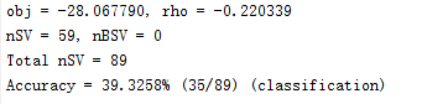
由以上散点图可以看出，分类结果偏差较大，分类正确率很低。数据分类存在很大的失误率。

数据归一化之后：

使用SVM的分类正确率为98.8764%。

在以上图中，红色部分代表预测测试数据集分类，X代表实际测试集分类结果，从图中我们可以直观的看出，只有一个预测数据分类错误，其余基本吻合分类结果。
由以上结果我们可以看出，SVM在该数据集的分类中的分类效果要好于KNN算法的分类效果。可能是由于该数据集的样本量较少，SVM算法可以解决小样本情况下的机器学习问题，提高泛化性能，可以避免神经网络结构选择和局部极小点问题。

如有问题，欢迎留言或者邮箱。